電気工学博士の雑記

電気工学の博士が徒然なるままに試した技術的なことをアウトプットする。

OpenModelicaを使ったPMSM電流制御シミュレーション入門

OpenModelica 技術記事

概要

この記事では誰でも無料で使用可能なオープンソースのOpenModelica OMEditを用いた、永久磁石同期モータ（Permanent Magnet Synchronous Motor; PMSM）の電流制御シミュレーションを紹介する。OpenModelicaは微分方程式のソルバーであり、数学モデルシステム、力学、熱力学、電磁気、電気回路などの幅広い分野のシミュレーションを複合的に行うことが可能である。OMEditを用いることで、GUI上で複数の機能ブロックを組み合わせるだけでシミュレーションを行うことができる。

最初にOMEdit上での設定を示した後に、PMSMのベクトル制御による電流フィードバックの理論の概要を簡単に説明する（詳細はこの記事末尾の参考サイトを見てほしい）。OMEditでモデルを構成する上で注意が必要なブロックを紹介した後に、シミュレーション結果を確認する。シミュレーションの細かな条件やパラメータなどは下記のPDFにまとめている。 https://app.box.com/s/84irpaixg9q6idrl20a3fb97lz41zxjk

OMEdit上でのPMSMモデル

背景

無料でパワーエレクトロニクスのシミュレーションが可能なシミュレータを探している中で、OpenModelicaを見つけた。その性能確認とソフトの使い方の学習の目的で、PMSMのシミュレーションを構成してみることにした。

OpenModelica

概要

OpenModelicaはModelica言語を用いた、オープンソース（OSMC Public License, EPL, GPL）の複雑な動的システムのシミュレーション・モデル作成・最適化・解析の環境であり、誰でも無料で様々な解析をすることができる。OpenModelicaは数学モデルシステム、力学、熱力学、電磁気、電気回路などの幅広い分野のシミュレーションを複合的に行うことが可能である。OpenModelicaの公式ページと、詳しく説明しているページを下記に記載するので、参考にしてほしい。

openmodelica.org virtualmbdlabmodelica.net 1dcae.com www.xsim.info

OMEdit

OpenModelicaのアプリケーションの1つであるOMEditは、matlab simlinkやscilab xcosのように、GUIを用いて視覚的に機能ブロックを組み合わせることで、シミュレーションモデルを構築できる。この記事ではOMEditを用いて、標準Modelicaライブラリ（Modelica Standard Library; MSL）のみを使うことでPMSMのシミュレーションモデルを構築して、その詳細を説明する。

シミュレーション内容

PMSM駆動システム

この記事では、空間ベクトル理論を用いて、永久磁石同期モータ（Permanent Magnet Synchronous Motor; PMSM）をインバータによって駆動するシステムを検討する。モータの負荷は定速度負荷とする。インバータは PWM Controller から受け取ったゲート信号 s_{u}、 s_{v}、 s_{w}にしたがって、必要な電圧を出力するように動作する。インバータの入力は直流電圧 V_{DC}であり、出力は三相電圧 v_{u}、 v_{v}、 v_{w}である。PMSMの前段には電流センサが設置させており、三相電流 i_{u}、 i_{v}、 i_{w}を検出する。PMSMの出力トルクは T_{m}、機械角速度は \omega_{m}とする。PMSMの機械角 \theta_{m}は位置センサにより検出される。

PMSM駆動システム

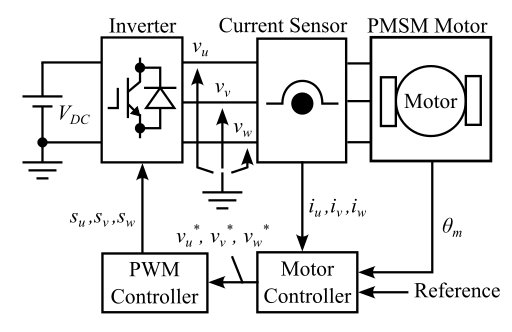
制御システムは電流・速度・トルク指令値（Reference）などを入力として、検出した i_{u}、 i_{v}、 i_{w}と \theta_{m}を用いて、PMSMを指令値に追従するように制御する。モータコントローラはPMSMを指令値に追従させるために必要なインバータ出力電圧指令値 v_{u}^{\ast}、 v_{v}^{\ast}、 v_{w}^{\ast}を出力し、PWMコントローラはこれらの指令値を実現するインバータのゲート信号 s_{u}、 s_{v}、 s_{w}を三角波比較法などを用いて生成する。

空間ベクトル理論

PMSMの制御ではゼロ相を制御しないため、クラーク変換を用いて三相電圧・電流をゼロ相とそれ以外の \alpha、 \beta相に分離する。クラーク変換の変換行列 ^{0\alpha\beta}\boldsymbol{C}_{uvw}は次式で定義される。

\displaystyle ^{0\alpha\beta}\boldsymbol{C}_{uvw} = \sqrt{\frac{2}{3}} \begin{bmatrix} \frac{1}{2} & \frac{1}{2} & \frac{1}{2} \\ \cos{\left( 0 \right)} & \cos{\left( \frac{2}{3} \pi \right)} & \cos{\left( -\frac{2}{3} \pi \right)} \\ \sin{\left( 0 \right)} & \sin{\left( \frac{2}{3} \pi \right)} & \sin{\left( -\frac{2}{3} \pi \right)} \end{bmatrix} = \sqrt{\frac{2}{3}} \begin{bmatrix} \frac{1}{2} & \frac{1}{2} & \frac{1}{2} \\ 1 & -\frac{1}{2} & -\frac{1}{2} \\ 0 & \frac{\sqrt{3}}{2} & -\frac{\sqrt{3}}{2} \end{bmatrix} \label{eq:Clark_conv_def}

クラーク逆変換 ^{uvw}\boldsymbol{C}_{0\alpha\beta}は ^{0\alpha\beta}\boldsymbol{C}_{uvw}を転置することで得られる。

\displaystyle ^{uvw}\boldsymbol{C}_{0\alpha\beta} = ^{0\alpha\beta}\boldsymbol{C}_{uvw}^{-1} = ^{0\alpha\beta}\boldsymbol{C}_{uvw}^{T}

クラーク変換により得られるゼロ相、 \alpha相、 \beta相の電圧・電流をそれぞれ v_{0}・ i_{0}、 v_{\alpha}・ i_{\alpha}、 v_{\beta}・ i_{\beta}とする。

\displaystyle \begin{bmatrix} v_{0} \\ v_{\alpha} \\ v_{\beta} \end{bmatrix} = ^{0\alpha\beta}\boldsymbol{C}_{uvw} \begin{bmatrix} v_{u} \\ v_{v} \\ v_{w} \end{bmatrix}, \quad \begin{bmatrix} i_{0} \\ i_{\alpha} \\ i_{\beta} \end{bmatrix} = ^{0\alpha\beta}\boldsymbol{C}_{uvw} \begin{bmatrix} i_{u} \\ i_{v} \\ i_{w} \end{bmatrix}

次に、得られた v_{\alpha}、 v_{\beta}、 i_{\alpha}、 i_{\beta}を回転子座標系に回転座標変換（dq変換）する。PMSMの極対数を p_{m}、電気角を \theta_{e}とすると、dq変換行列は次式で与えられる。

\displaystyle \begin{align} \theta_{e} &= p_{m} \theta_{m} \\ ^{dq}\boldsymbol{C}_{\alpha\beta} &= \begin{bmatrix} \cos{\theta_{e}} & \sin{\theta_{e}} \\ -\sin{\theta_{e}} & \cos{\theta_{e}} \end{bmatrix} \label{eq:dq_conv_def} \\ ^{\alpha\beta}\boldsymbol{C}_{dq} &= ^{dq}\boldsymbol{C}_{\alpha\beta}^{-1} = ^{dq}\boldsymbol{C}_{\alpha\beta}^{T} \label{eq:dq_inv_conv_def} \end{align}

逆dq変換行列 ^{\alpha\beta}\boldsymbol{C}_{dq}は ^{dq}\boldsymbol{C}_{\alpha\beta}に \theta_{e} = -\theta_{e}を代入したものであり、dq変換の逆回転の変換である。よってdq座標系での \alpha\beta電圧・電流 v_{d}、 v_{q}、 i_{d}、 i_{q}は次式で表される。

\displaystyle \begin{bmatrix} v_{d} \\ v_{q} \end{bmatrix} = ^{dq}\boldsymbol{C}_{\alpha\beta} \begin{bmatrix} v_{\alpha} \\ v_{\beta} \end{bmatrix}, \quad \begin{bmatrix} i_{d} \\ i_{q} \end{bmatrix} = ^{dq}\boldsymbol{C}_{\alpha\beta} \begin{bmatrix} i_{\alpha} \\ i_{\beta} \end{bmatrix}

PMSM の数理モデル

uvw座標系において1相当たりの配線抵抗を R_{uvw}、永久磁石による磁束の振幅を \Phi_{uvw}、電気角速度を \omega_{e}とすると、PMSMの数理モデルは次式で表される。

\displaystyle \begin{align} \begin{bmatrix} v_{u} \\ v_{v} \\ v_{w} \end{bmatrix} &= \begin{bmatrix} R_{uvw} & 0 & 0 \\ 0 & R_{uvw} & 0 \\ 0 & 0 & R_{uvw} \end{bmatrix} \begin{bmatrix} i_{u} \\ i_{v} \\ i_{w} \end{bmatrix} + \boldsymbol{L} \frac{d}{dt} \begin{bmatrix} i_{u} \\ i_{v} \\ i_{w} \end{bmatrix} + \omega_{e} \begin{bmatrix} \Phi_{uvw} \sin{\left( \omega_{e} t \right)} \\ \Phi_{uvw} \sin{\left( \omega_{e} t - \frac{2}{3}\pi \right)} \\ \Phi_{uvw} \sin{\left( \omega_{e} t + \frac{2}{3}\pi \right)} \end{bmatrix} \\ \omega_{e} &= \frac{d \theta_{e}}{dt} \end{align}

ここで \boldsymbol{L}はPMSMのインダクタンス行列であり、PMSMの数理モデルの電流微分の係数行列である。上式をdq座標系で表した等価な方程式は次式で表される。

\displaystyle \begin{align} \begin{bmatrix} v_{d} \\ v_{q} \end{bmatrix} &= \begin{bmatrix} R_{uvw} + L_{d} \frac{d}{dt} & -\omega_{e} L_{q} \\ \omega_{e} L_{d} & R_{uvw} + L_{q} \frac{d}{dt} \end{bmatrix} \begin{bmatrix} i_{d} \\ i_{q} \end{bmatrix} + \begin{bmatrix} 0 \\ \omega_{e} \Phi_{dq} \end{bmatrix} \label{eq:PMSM_vi_dq} \\ \Phi_{dq} &= \sqrt{\frac{3}{2}} \Phi_{uvw} \label{eq:Phi_uvw2dq} \end{align}

ここで L_{d}、 L_{q}はd軸・q軸インダクタンスである。dq座標系での配線抵抗はuvw座標系と同じ値 R_{uvw}となるのに対して、dq座標系での永久磁石の磁束 \Phi_{dq}はuvw座標系磁束 \Phi_{uvw}の \sqrt{3/2}となることに注意が必要である。

PMSM 制御システム

ここでは古典的な比例積分（PI）制御を適用した電流フィードバック制御をシミュレーションする。PMSMの電流フィードバック制御では、干渉項と永久磁石による誘起電圧項をフィードフォワードすることによって補償する。上図は制御ブロック図であり、 i_{d}^{\ast}、 i_{q}^{\ast}、 v_{d}^{\ast}、 v_{q}^{\ast}は i_{d}、 i_{q}、 v_{d}、 v_{q}の司令値である。上図の i_{d}、 i_{q}、 \omega_{e}はセンサなどにより検出する。司令値 v_{d}^{\ast}、 v_{q}^{\ast}は逆dq変換と逆クラーク変換により、 v_{u}^{\ast}、 v_{v}^{\ast}、 v_{w}^{\ast}に変換して PWM Controller に転送する。

PMSM制御システム

OMEditのPMSM駆動モデルの構築

前述したPMSMドライブ回路とPMSMの制御システムのモデルをOMEditで作成すればよい。ここでは、構築したPMSMのOMEditシミュレーションモデルで注意が必要な要素のみの簡潔な説明を示す（詳細は Modelica Documentation）。 ToSpacePhasor ブロックを用いてクラーク変換を行う場合、 ToSpacePhasor ブロックの出力値に \sqrt{3/2}を乗ずる必要がある。同様に FromSpacePhasor ブロックを使って逆クラーク変換を行うには、ゼロシーケンス値をゼロ相の 1/2として、ブロックの出力値に \sqrt{2/3}を乗ずる。

.Modelica.Electrical.Analog.Ideal.IdealOpeningSwitch
理想的な開閉スイッチであり、そのスイッチング動作は，入力 boolean 信号により制御される。 boolean 信号が True のときスイッチは OFF となる。
.Modelica.Electrical.Polyphase.Basic.PlugToPin_p
plug_p （多相回路）の k ピンを pin_p （単相回路）に接続し、plug_p の他のピンは未接続（開放）にする。
.Modelica.Electrical.Machines.SpacePhasors.Blocks.ToSpacePhasor
多相電圧または電流をスペースフェーザおよびゼロシーケンス値に変換する。三相の場合には、三相入力を [x\_{u}, x\_{v}, x\_{w}]、スペースフェーザを [x\_{\alpha}, x\_{\beta}]、ゼロシーケンス値を x\_{0}とすると、下式の変換を行う。
\begin{align*} \begin{bmatrix} x_{\alpha} \\ x_{\beta} \end{bmatrix} &= \frac{2}{3} \begin{bmatrix} \cos{\left( 0 \right)} & \cos{\left( \frac{2}{3} \pi \right)} & \cos{\left( -\frac{2}{3} \pi \right)} \\ \sin{\left( 0 \right)} & \sin{\left( \frac{2}{3} \pi \right)} & \sin{\left( -\frac{2}{3} \pi \right)} \end{bmatrix} \begin{bmatrix} x_{u} \\ x_{v} \\ x_{w} \end{bmatrix}\\ x_{0} &= \frac{x_{u} + x_{v} + x_{w}}{3} \end{align*}
.Modelica.Electrical.Machines.SpacePhasors.Blocks.FromSpacePhasor
スペースフェーザおよびゼロシーケンス値から多相電圧または電流へ変換する。三相の場合には、三相出力を [x\_{u}, x\_{v}, x\_{w}]、スペースフェーザを [x\_{\alpha}, x\_{\beta}]、ゼロシーケンス値を x\_{0}とすると、下式の変換を行う。
\begin{equation*} \begin{bmatrix} x_{u} \\ x_{v} \\ x_{w} \end{bmatrix} =\begin{bmatrix} x_{0} \\ x_{0} \\ x_{0} \end{bmatrix} + \begin{bmatrix} \cos{\left( 0 \right)} & -\sin{\left( 0 \right)} \\ \cos{\left( -\frac{2}{3} \pi \right)} & -\sin{\left( -\frac{2}{3} \pi \right)} \\ \cos{\left( \frac{2}{3} \pi \right)} & -\sin{\left( \frac{2}{3} \pi \right)} \end{bmatrix}\begin{bmatrix} x_{\alpha} \\ x_{\beta} \end{bmatrix} \end{equation*}
.Modelica.Electrical.Machines.SpacePhasors.Blocks.Rotator
スペースフェーザ（電圧または電流）を数学的に負方向（反時計回り）に、入力された角度だけ回転させる。

シミュレーション

シミュレーションの細かな条件やパラメータなどは下記のPDFにまとめている。 https://app.box.com/s/84irpaixg9q6idrl20a3fb97lz41zxjk

OMEditのシミュレーションの刻み幅は 2\mathrm{\mu s}とした。シミュレーション結果を下記に示す。上から順にdq軸電流 i_{d}、 i_{q}とその司令値 i_{d}^{\ast}、 i_{q}^{\ast}、uvw相電流 i_{u}、 i_{v}、 i_{w}、uvw相電圧 v_{u}、 v_{v}、 v_{w}、三角波比較での三角波 triと変調波 d_{u}、 d_{v}、 d_{w}の波形である。dq軸電流は司令値に追従しており、PMSMの電流制御を実現していることがわかる。uvw相電圧は階段状の波形であり、インバータのPWM制御によりPMSMを制御している。 i_{d}、 i_{q}のリプルはスイッチングに起因する。

シミュレーション結果

まとめ

PMSMの大まかなシミュレーションは問題なく動いたが、パラメータによっては収束しない場合がある。特にスイッチング時に微分方程式の解が不安定になるので、シミュレーションを動かすためのノウハウを蓄積する必要があるかもしれない。シミュレーションを構成すること自体は簡単にできるので、これからも使ってみようと思う。

参考